01 Introduction

On January 4th, a research paper titled “Observation of localization of light in linear photonic quasicrystals with diverse rotational symmetries” was published in the journal Nature Photonics from a research group led by Professor Fangwei Ye from Shanghai Jiao Tong University. This study utilized the “optical induction” method to create a series of optical quasicrystal structures and observed the phenomenon of spontaneous localization of light within them. The study also revealed a one-to-one correspondence between the threshold at which this localization occurs and the symmetry of the quasicrystals.

02 Research Background

Quantum mechanics posits that all particle behaviors are described by waves, and the evolution of waves in a potential field strongly depends on the spatial structure of that field. When the potential field has a periodic structure, waves tend to diffracts/disperse; in contrast, in a random structure (either one-dimensional or two-dimensional), waves invariably localize. To date, research on periodic and random structures has been systematic and profound. However, between these two types of structures lies a unique and significant structure——the quasicrystal. Understanding of quasicrystals is relatively lacking compared to the other two. Quasicrystals lack translational symmetry but possess unique rotational symmetries: whereas periodic structures can only exhibit two-fold, three-fold, four-fold, and six-fold rotational symmetries, quasicrystals can exhibit five-fold, seven-fold, eight-fold, or even higher orders of rotational symmetry (see Figure 1). Thus, an important scientific question arises – how do waves evolve in quasicrystal structures? Will they always expand as in periodic systems, or will they localize as in random systems?

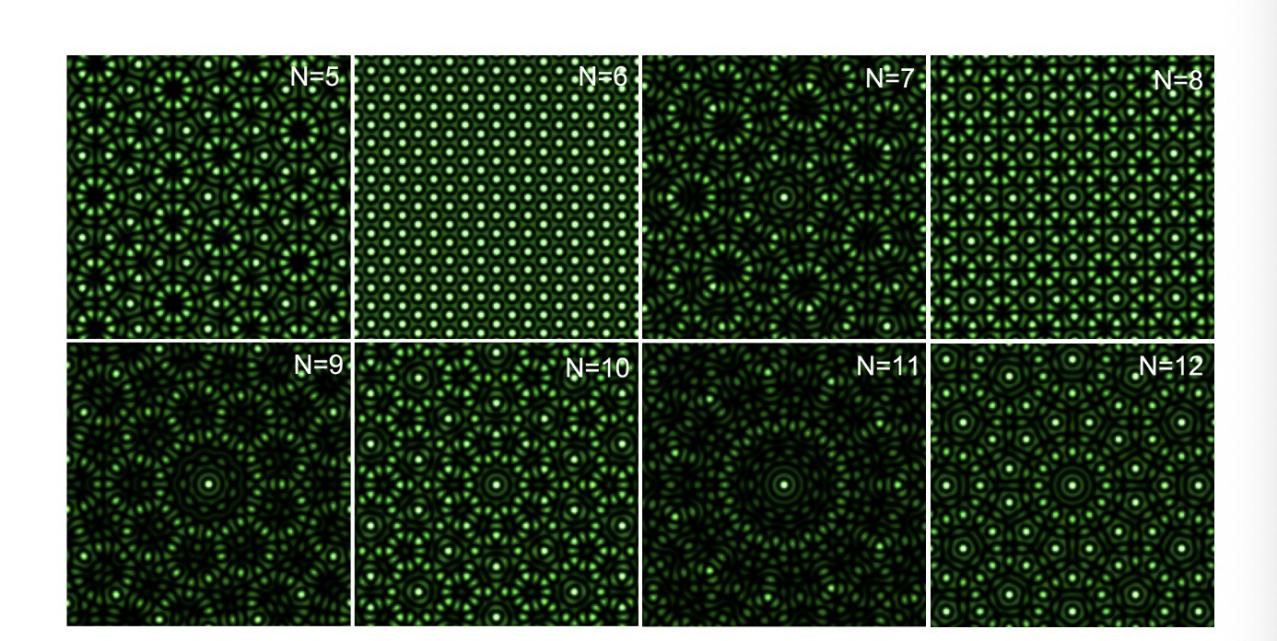
Figure 1. Two-dimensional photonic quasicrystal diagram. Presented here are quasicrystal structures with rotational symmetries starting from N=5 up to N=12. However, note that the N=6 structure is a periodic structure (not a quasicrystal structure).

In previous research reports, this significant scientific question has been addressed, with researchers indeed observing the localization of light waves in quasicrystal systems [see Nature 440, 1166 (2006) and Science 332, 1541 (2011)]. However, the quasicrystal structures studied in these works were not “pure” quasicrystals but were combined with nonlinear optical responses or random effects. Therefore, whether “pure” optical quasicrystal structures can support the localization of light remains an unsolved mystery.

03 Research Innovation

The research group led by Professor Fangwei Ye at Shanghai Jiao Tong University has long been dedicated to exploring the unique optical properties and light control methods offered by quasiperiodic and aperiodic photonic lattices, and they have provided a definitive answer to the important scientific question: Can quasicrystals localize light? Experimentally, they used the “optical induction” method to inscribe a series of optical quasicrystal structures with various rotational symmetries (denoted by the number N) in a photosensitive material called strontium barium niobate (SBN), ranging from five-fold to twelve-fold symmetries(as shown in Figure 1). Then, a beam as the signal light was introduced into these quasicrystal structures and observed its propagation and evolution, discovering that signal light can indeed localize in “pure” quasicrystal structures. However, this localization only occurs when the modulation of the refractive index in the quasicrystal structure (controlled experimentally by applying an external electric field E) exceeds a certain level: due to the electro-optic effect, as the applied electric field E increases, the depth of refractive index modulation in the quasicrystal structure also increases correspondingly. When E exceeds a specific value (denoted as ), the probe light transitions from a “delocalized” state to a “localized” state, indicating a phase transition. Interestingly, for quasicrystals with different rotational symmetry numbers N, the critical voltage  for the “delocalized-localized” phase transition of the probe light also varies. For example, Figure 2 presents a comparison of light propagation in quasicrystals with five-fold and eight-fold symmetries: at an applied electric field of E=400 V/mm, the probe light in the five-fold quasicrystal has already undergone a phase transition to the localized phase, while in the eight-fold quasicrystal, it remains in the delocalized state, indicating that light is more readily localized in five-fold quasicrystals compared to eight-fold ones.

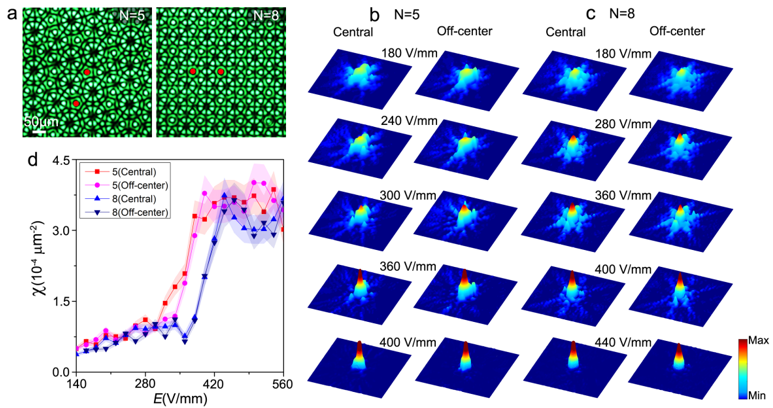
Figure 2: The probe light incident on the input facet of quasicrystals with N=5 and N=8 [marked by the red dots in figure (a)], and the observed output intensity distributions of probe beam after propagating in 2-cm-long quasicrystal lattices (b, c). It can be observed that with the continuous increase in the applied electric field, the output light spot transitions from an initial delocalized state to a localized state through a phase change. Comparing the phase transition of N=5 and N=8 quasicrystals (d), it is evident that localization occurs earlier in N=5 than in N=8.

Figure 2 also shows the evolution of the probe light under different excitation conditions within the same quasicrystal, revealing that the light beams have the same phase transition point  under various excitation conditions, proving that the delocalization to localization phase transition is an intrinsic property of the quasicrystal structure, independent of the probe light's excitation location.

The comparative results of Figure 2 might give the impression that quasicrystals with a higher symmetry number N are less likely to localize light waves, but this is actually a misconception. The study found that the phase transition point is related to the odd or even nature of the rotational symmetry number N. Quasicrystals with N=5, 7, 9, 11... form one group, and their phase transition points decrease successively with the increase in N: the 7-fold quasicrystal localizes light more easily than the 5-fold, the 9-fold more easily than a 7-fold structures, and so on. Correspondingly, N=8, 10, 12, 14... form another group, and their phase transition points also decrease as N increases [Figure 3 (a, b)]. If the odd and even groups of quasicrystals are combined and arranged in order of increasing ease of light localization, the correct sequence is found to be 8, 5, 10, 12, 7, 9, 11..., which seems like a random series (although the numbers in this series are overall increasing). Surprisingly, this sequence precisely corresponds to the “spatial nonuniformity” of the quasicrystals [Figure 3 (c)]. The spatial nonuniformity  of the quasicrystal is determined by the average deviation of the refractive index modulation relative to a reference point:  equals zero indicates spatial uniformity, and the larger the , the more nonuniform the spatial distribution. Hence, Figure 3 (c) reveals a very intuitive result: the more “nonuniform” the quasicrystal, the easier to localize light.

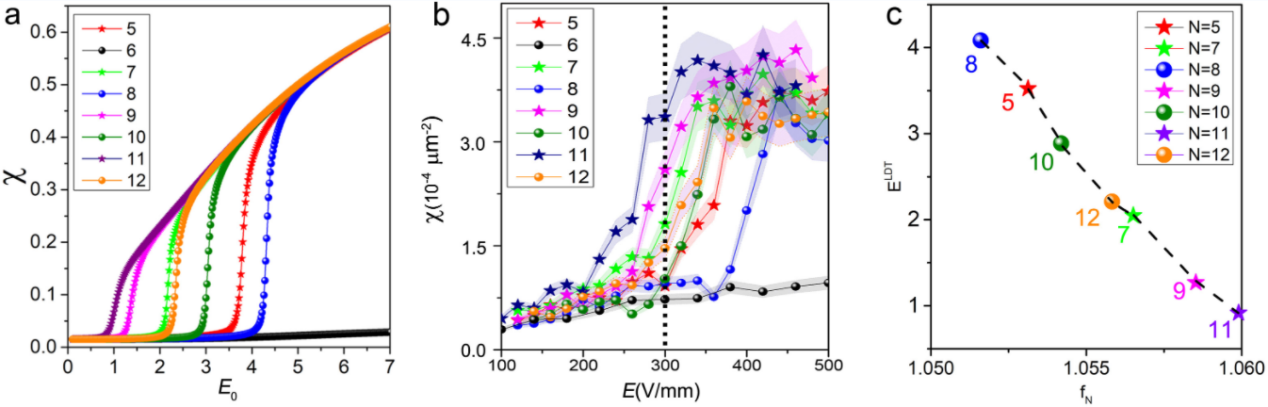
Figure 3: The variation of the beam form factor χ with the applied electric field (a: simulation results; b: experimental results). The form factor χ is inversely proportional to the beam width, hence the increase in χ represents the phase transition of the beam from “dispersion” to “localization”. (c) The relationship between the phase transition point  of various order quasicrystals and the “spatial nonuniformity”  of the quasicrystals.

04 Conclusion and Outlook

This study addresses the localization of light in an important optical structure——the photonic quasicrystal, and for the first time discovers the localization-delocalization phase transition rule of light in quasicrystals, revealing the fundamental connection between wave localization in quasicrystals and their symmetry. The first author of the paper, postdoctoral researcher Peng Wang, believes, “Quasicrystals are a type of crystal structure with a certain degree of disorder. Their spatial structure is not as completely symmetrical and periodic as that of crystals, hence this study represents a clear physical law of light localization discovered in such disordered structures.” Co-first author and postdoctoral researcher Qidong Fu, discussing the significance of this discovery, said, “This finding provides a new method for the localization and manipulation of light, and also offers insights for the localization and control of more general types of waves, such as electromagnetic waves, sound waves, and matter waves.”

Paper link: https://www.nature.com/articles/s41566-023-01350-6